Simulation Primer
An Introduction to Basic Simulation Concepts
What is Simulation?
The term simulation is used in different ways by different people. As used here, simulation is defined as the process of creating a model (i.e., an abstract representation or facsimile) of an existing or proposed system (e.g., a project, a business, a mine, a watershed, a forest, the organs in your body) in order to identify and understand those factors which control the system and/or to predict (forecast) the future behavior of the system. Almost any system which can be quantitatively described using equations and/or rules can be simulated.
The Purpose of Simulation
We frequently look into the future of mankind and see dangers... Looking into the future may be one of the reasons that brains evolved in the first place.Richard Dawkins
The underlying purpose of simulation is to shed light on the underlying mechanisms that control the behavior of a system. More practically, simulation can be used to predict (forecast) the future behavior of a system, and determine what you can do to influence that future behavior. That is, simulation can be used to predict the way in which the system will evolve and respond to its surroundings, so that you can identify any necessary changes that will help make the system perform the way that you want it to.
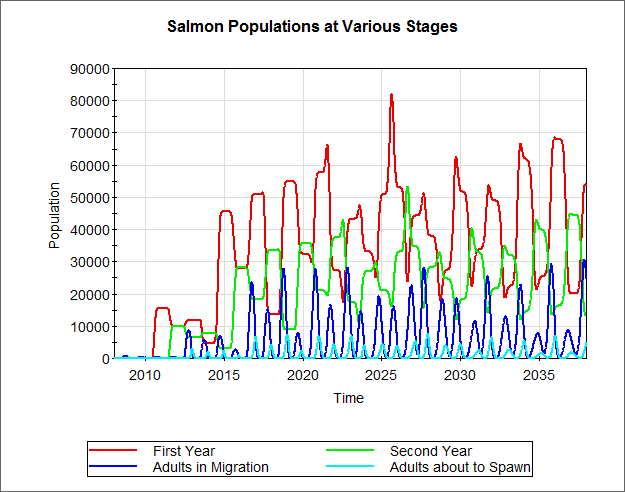
For example, a fisheries biologist could dynamically simulate the salmon population in a river in order to predict changes to the population, and quantitatively understand the impacts on the salmon of possible actions (e.g., fishing, loss of habitat) to ensure that they do not go extinct at some point in the future.
The Power of Simulation
Simulation is a powerful and important tool because it provides a way in which alternative designs, plans and/or policies can be evaluated without having to experiment on a real system, which may be prohibitively costly, time-consuming, or simply impractical to do. That is, it allows you to ask "What if?" questions about a system without having to experiment on the actual system itself (and hence incur the costs of field tests, prototypes, etc.).
Addressing Risk and Uncertainty Using Probabilistic Simulation
Our knowledge of the way things work, in society or nature, comes trailing clouds of vagueness. Vast ills have followed a belief in certainty.Kenneth Arrow (Nobel Laureate, Economics, 1972)
Although simulation can be a valuable tool for better understanding the underlying mechanisms that control the behavior of a system, using simulation to make predictions of the future behavior of a system can be difficult. This is because, for most real-world systems, at least some of the controlling parameters, processes and events are often stochastic, uncertain and/or poorly understood. The objective of many simulations is to identify and quantify the risks associated with a particular option, plan or design. Simulating a system in the face of such uncertainty and computing such risks requires that the uncertainties be quantitatively included in the calculations.
Deterministic Simulation
Many simulation tools and approaches are deterministic. In a deterministic simulation, the input parameters for a model are represented using single values (which typically are described either as "the best guess" or "worst case" values). Unfortunately, this kind of simulation, while it may provide some insight into the underlying mechanisms, is not well-suited to making predictions to support decision-making, as it cannot quantitatively address the risks and uncertainties that are inherently present.
Probabilistic Simulation
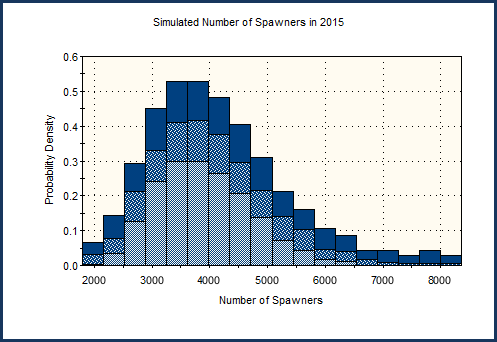
It is possible, however, to quantitatively represent uncertainties in simulations. Probabilistic simulation is the process of explicitly representing these uncertainties by specifying inputs as probability distributions. If the inputs describing a system are uncertain, the prediction of future performance is necessarily uncertain. That is, the result of any analysis based on inputs represented by probability distributions is itself a probability distribution. Hence, whereas the result of a deterministic simulation of an uncertain system is a qualified statement ("if we build the dam, the salmon population could go extinct"), the result of a probabilistic simulation of such a system is a quantified probability ("if we build the dam, there is a 20% chance that the salmon population will go extinct"). Such a result (jn this case, quantifying the risk of extinction) is typically much more useful to decision-makers who might utilize the simulation results.
Monte Carlo Simulation
In order to compute the probability distribution of predicted performance, it is necessary to propagate (translate) the input uncertainties into uncertainties in the results. A variety of methods exist for propagating uncertainty. One common technique for propagating the uncertainty in the various aspects of a system to the predicted performance (and the one used by GoldSim) is Monte Carlo simulation. In Monte Carlo simulation, the entire system is simulated a large number (e.g., 1000) of times. Each simulation is equally likely, and is referred to as a realization of the system. For each realization, all of the uncertain parameters are sampled (i.e., a single random value is selected from the specified distribution describing each parameter). The system is then simulated through time (given the particular set of input parameters) such that the performance of the system can be computed. This results in a large number of separate and independent results, each representing a possible “future” for the system (i.e., one possible path the system may follow through time). The results of the independent system realizations are assembled into probability distributions of possible outcomes.
Problem Solving and Decision Making with Simulation Software
Simulation is a decision analysis and support tool. Simulation software allows you to evaluate, compare and optimize alternative designs, plans and policies. As such, it provides a tool for explaining and defending decisions to various stakeholders.
The ability to define what may happen in the future and to choose among alternatives lies at the heart of contemporary societies.Peter Bernstein, Against the Gods: The Remarkable Story of Risk
Simulation should be used when the consequences of a proposed action, plan or design cannot be directly and immediately observed (i.e., the consequences are delayed in time and/or dispersed in space) and/or it is simply impractical or prohibitively expensive to test the alternatives directly. For example, when implementing a strategic plan for a company, the impacts are likely to take months (or years) to materialize.
Simulation is particularly valuable when there is significant uncertainty regarding the outcome or consequences of a particular alternative under consideration. Probabilistic simulation allows you deal with this uncertainty in a quantifiable way.
Perhaps most importantly, simulation should be used when the system under consideration has complex interactions and requires the input from multiple disciplines. In this case, it is difficult for any one person to easily understand the system. A simulation model can act as the framework to integrate the various components in order to better understand their interactions. As such, it becomes a management tool that keeps you focused on the "big picture" without getting lost in unimportant details.
Types of Simulation Tools
Because simulation is such a powerful tool to assist in understanding complex systems and to support decision-making, a wide variety of approaches and tools exist.
Many special purpose simulators exist to simulate very specific types of systems. For example, tools exist for simulating the movement of water (and contaminants) in an estuary, the evolution of a galaxy, or the exchange rates for a set of currencies. The key attribute of these tools is that they are highly specialized to solve a particular type of problem. In many cases, these tools require great subject-matter expertise to use. In other cases, however, the system being simulated may be so highly specified that using the tools is quite simple (i.e., the user is presented with a very limited number of options).
Other tools are not specialized to a particular type of problem. Rather, they are "tool kits" or general purpose frameworks for simulating a wide variety of systems. There are a variety of such tools, each tailored for a specific type of problem. What they all have in common, however, is that they allow the user to model how a system might evolve or change over time. Such frameworks can be thought of as high-level programming languages that allow the user to simulate many different kinds of systems in a flexible way.
Spreadsheets
Perhaps the simplest and most broadly used general purpose simulator is the spreadsheet. Although spreadsheets are inherently limited by their structure in many ways (e.g., representing complex dynamic processes is difficult, they cannot display the model structure graphically, and they require special add-ins to represent uncertainty), because of their ubiquity, they are very widely used for simple simulation projects (particularly in the business world).
Other general purpose tools exist that are better able to represent complex dynamics, as well as provide a graphical mechanism for viewing the model structure (e.g., an influence diagram or flow chart of some type). Although these tools are generally harder to learn to use than spreadsheets (and are typically more expensive), these advantages allow them to realistically simulate larger and more complex systems than can be done in a spreadsheet.
Discrete Event Simulators
These tools rely on a transaction-flow approach to modeling systems. Models consist of entities (units of traffic), resources (elements that service entities), and control elements (elements that determine the states of the entities and resources). Discrete simulators are generally designed for simulating processes such as call centers, factory operations, and shipping facilities in which the material or information that is being simulated can be described as moving in discrete steps or packets. They are not meant to model the movement of continuous material (e.g., water) or represent continuous systems that are represented by differential equations.
Agent-Based Simulators
This is a special class of discrete event simulator in which the mobile entities are known as agents. Whereas in a traditional discrete event model the entities only have attributes (properties that may control how they interact with various resources or control elements), agents have both attributes and methods (e.g., rules for interacting with other agents). An agent-based model could, for example, simulate the behavior of a population of animals that are interacting with each other.
Continuous Simulators
This class of tools solves differential equations that describe the evolution of a system using continuous equations. These type of simulators are most appropriate if the material or information that is being simulated can be described as evolving or moving smoothly and continuously, rather than in infrequent discrete steps or packets. For example, simulation of the movement of water through a series of reservoirs and pipes can most appropriately be represented using a continuous simulator. Continuous simulators can also be used to simulate systems consisting of discrete entities if the number of entities is large so that the movement can be treated as a flow. A common class of continuous simulators are system dynamics tools, based on the standard stock and flow approach developed by Professor Jay W. Forrester at MIT in the early 1960s.
Hybrid Simulators
These tools combine the features of continuous simulators and discrete simulators. That is, they solve differential equations, but can superimpose discrete events on the continuously varying system. GoldSim is a hybrid simulator.
Learn More
- Read a guide to selecting a simulation tool that best meets your needs
- Learn more about GoldSim
